A 1 Matriks

Oleh karena itu matriks a dikatakan berordo 4 u 2. Matriks a terdiri atas 4 baris dan 2 kolom. Sementara untuk matriks kolom merupakan sebuah matriks yang hanya mempunyai satu kolom saja.

jocurile olimpice de iarna juventus vs real madrid 2020 match date la multi ani bunica mea judetele romaniei harta romaniei orase si comune la multi ani camelia ziua de nastere karl heinz rummenigge bayern munich jocuri de mers la cumparaturi juventus real madrid champion league final turin 2017

Matriks Elementer Dan Invers

Contoh Dan Penyelesain Matrix Invers Matriks

Tentukan Invers Dari Matriks Berikut A 1 3 2 7 Brainly Co Id

Diketahui Matriks A 1 2 3 4 Brainly Co Id

Menentukan Invers Suatu Matriks Ilmu Hitung

Jika Matriks A 1 2 1 3 B 3 1 2 4 Dan C Memenuhi Ac B Matriks C Adalah Brainly Co Id

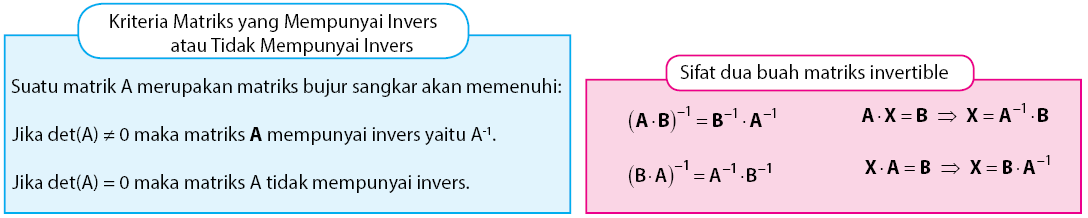
Tidak semua matriks memiliki invers hanya matriks persegi dengan determinan tidak sama dengan nol yang memiliki invers.

A 1 matriks. Syarat suatu matriks a mempunyai invers. Secara umum invers dari matriks persegi a atau ditulis a 1 adalah sebagai berikut. Supaya dapat menyelesaikan persamaan matriks yang berbentuk xa b bisa ditentukan dengan cara mengalikan kedua ruasnya dari kanan. Matriks a dan b adalah matriks yang saling invers.

Langkah kedua kita cari kofaktor matriks bagian dari matriks a c ij cij 1 i j m ij dan m ij det a ij dengan a ij merupakan matriks bagian dari matriks a yang diperoleh dengan menghilangkan baris ke i dan kolom ke j. A 1 4 atau b 3 7 9 merupakan matriks baris. A 1 x adj a jika determinan atau det a sama dengan 0 maka a 1 x adj a dari persamaan di atas maka bisa di simpulkan bahwa matriks singular dikatakan sebagai matriks yang tidak mempunyai nilai karena nilai determinan a 0 akan menghasilkan a invers tidak berhingga. Oleh karena itu dikatakan matriks a sebagai matriks nonsingular.

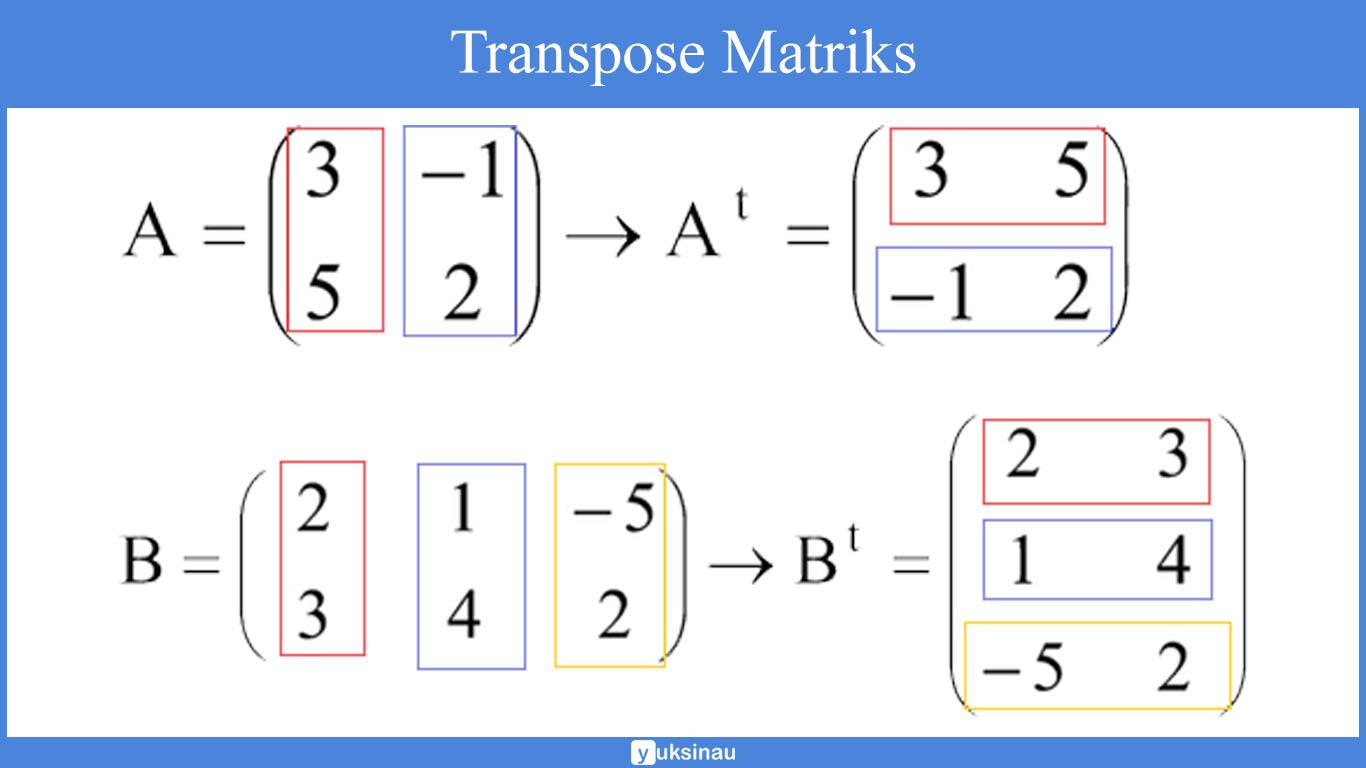
Invers dari matriks a dinotasikan dengan a 1. Matriks baris merupakan sebuah matriks yang hanya mempunyai satu baris saja. Ax b a 1 ax a 1 b a 1 a x a 1 b ix a 1 b x a 1 b dari persamaan yang terakhir ini nampaknya bahwa kedua ruas yang dikalikan dari kiri oleh a 1 sampai diperoleh bentuk penyelesaiannya x a 1 b. Sebelumnya kita telah memilih elemen elemen pada baris ke 1 yaitu a 11 a 12 dan a 13.

Adapun bilangan bilangan yang terdapat dalam matriks dinamakan elemen matriks. Jika a 0 maka matriks a tidak mempunyai invers. Oleh karena itu dikatakan matriks a sebagai matriks singular. Jika a 0 maka matriks a mempunyai invers.

Oke coba kamu perhatikan baik baik ya.